Quantum computing -- deuteron
Article
- E. F. Dumitrescu, A. J. McCaskey, G. Hagen, G. R. Jansen, T. D. Morris, T. Papenbrock, R. C. Pooser, D. J. Dean, and P. Lougovski
Cloud Quantum Computing of an Atomic Nucleus
Phys. Rev. Lett. 120, 210501 (2018) article – arXiv
Details
The article is based on the Unitary Coupled Clusters (UCC) ansatz (see link for details) which can be obtained using the following circuit:
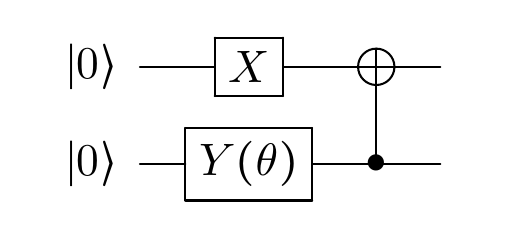
This results in the following wave function after the first operations:
\[\begin{equation} \ket{ {\Psi}_{\text{UCC}} } = \cos(\frac{\theta}{2}) \ket{10} + \sin(\frac{\theta}{2}) \ket{01} \end{equation}\]The UCC ansatz wave function looks like a parametrized Bell state.
Hamiltonian on two qubits
Once the ansatz is set, one can apply the Hamiltonian derived in the article:
\(\begin{equation} {H}_{2} = a I + b {Z}_{0} + c {Z}_{1} + d ({X}_{0} {X}_{1} + {Y}_{0} {Y}_{1}) \end{equation}\)
where ${ a }$, ${ b }$, ${ c }$, and ${ d }$ are constants given by the problem (see article). The identity ${ I }$ and the ${ Z }$ gates are trivial while the two-qubit gates ${ XX }$ and ${ YY }$ need to be computed before. The effect of each term of the Hamiltonian on the wave function is:
\begin{equation} \begin{aligned} b Z_0 \ket{ {\Psi}_{\text{UCC}} } &= b \left( \cos(\frac{\theta}{2}) \begin{pmatrix} 1 & 0 \\\
0 & -1 \end{pmatrix} \begin{pmatrix} 0 \\\
1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\\
0 \end{pmatrix} + \sin(\frac{\theta}{2}) \begin{pmatrix} 1 & 0 \\\
0 & -1 \end{pmatrix} \begin{pmatrix} 1 \\\
0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\\
1 \end{pmatrix} \right) \\\
&= -b \cos(\frac{\theta}{2}) \ket{10} + b \sin(\frac{\theta}{2}) \ket{01} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} c Z_1 \ket{ {\Psi}_{\text{UCC}} } &= c \left( \cos(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
1 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\\
0 & -1 \end{pmatrix} \begin{pmatrix} 1 \\\
0 \end{pmatrix} + \sin(\frac{\theta}{2}) \begin{pmatrix} 1 \\\
0 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\\
0 & -1 \end{pmatrix} \begin{pmatrix} 0 \\\
1 \end{pmatrix} \right) \\\
&= c \cos(\frac{\theta}{2}) \ket{10} -c \sin(\frac{\theta}{2}) \ket{01} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} d X_0 X_1 \ket{ {\Psi}_{\text{UCC}} } &= d \begin{pmatrix} 0 & 0 & 0 & 1 \\\
0 & 0 & 1 & 0 \\\
0 & 1 & 0 & 0 \\\
1 & 0 & 0 & 0 \end{pmatrix} \left( \cos(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
0 \\\
1 \\\
0 \end{pmatrix} \sin(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
1 \\\
0 \\\
0 \end{pmatrix} \right) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} d Y_0 Y_1 \ket{ {\Psi}_{\text{UCC}} } &= d \begin{pmatrix} 0 & 0 & 0 & -1 \\\
0 & 0 & 1 & 0 \\\
0 & 1 & 0 & 0 \\\
-1 & 0 & 0 & 0 \end{pmatrix} \left( \cos(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
0 \\\
1 \\\
0 \end{pmatrix} \sin(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
1 \\\
0 \\\
0 \end{pmatrix} \right) \end{aligned} \end{equation}
\begin{equation} \begin{aligned} d (X_0 X_1 + Y_0 Y_1) \ket{ {\Psi}_{\text{UCC}} } &= d \cos(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
1 \\\
0 \\\
0 \end{pmatrix} +d\sin(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
0 \\\
1 \\\
0 \end{pmatrix} +d\cos(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
1 \\\
0 \\\
0 \end{pmatrix} +d\sin(\frac{\theta}{2}) \begin{pmatrix} 0 \\\
0 \\\
1 \\\
0 \end{pmatrix} \end{aligned} \end{equation}
Adding the contribution from the identity one obtains:
\[\begin{equation} H_2 \ket{ {\Psi}\_{\text{UCC}} } = \left[ (a+b-c) \sin(\frac{\theta}{2}) + 2d \cos(\frac{\theta}{2}) \right] \ket{01} + \left[ (a-b+c) \cos(\frac{\theta}{2}) + 2d \sin(\frac{\theta}{2}) \right] \ket{10} \end{equation}\]One can then compute the average energy of the system as:
\begin{equation} \begin{aligned} & \bk{ {\Psi}_{\text{UCC}} }{ H_2 }{ {\Psi}_{\text{UCC}} } \\\
&= \left( \cos(\frac{\theta}{2}) \bra{10} + \sin(\frac{\theta}{2}) \bra{01} \right) \left( \left[ (a+b-c) \sin(\frac{\theta}{2}) + 2d \cos(\frac{\theta}{2}) \right] \ket{01} + \left[ (a-b+c) \cos(\frac{\theta}{2}) + 2d \sin(\frac{\theta}{2}) \right] \ket{10} \right) \\\
&= \cos(\frac{\theta}{2}) \left( (a-b+c) \cos(\frac{\theta}{2}) + 2d \sin(\frac{\theta}{2}) \right) + \sin(\frac{\theta}{2}) \left( (a+b-c) \sin(\frac{\theta}{2}) + 2d \cos(\frac{\theta}{2}) \right) \\\
&= a + (c-b) \left( { \cos(\frac{\theta}{2}) }^{2} - { \sin(\frac{\theta}{2}) }^{2} \right) + 4d \sin(\frac{\theta}{2}) \cos(\frac{\theta}{2}) \\\
&= a + (c-b) \cos(\theta) + 4d \sin(\frac{\theta}{2}) \cos(\frac{\theta}{2}) \end{aligned} \end{equation}
